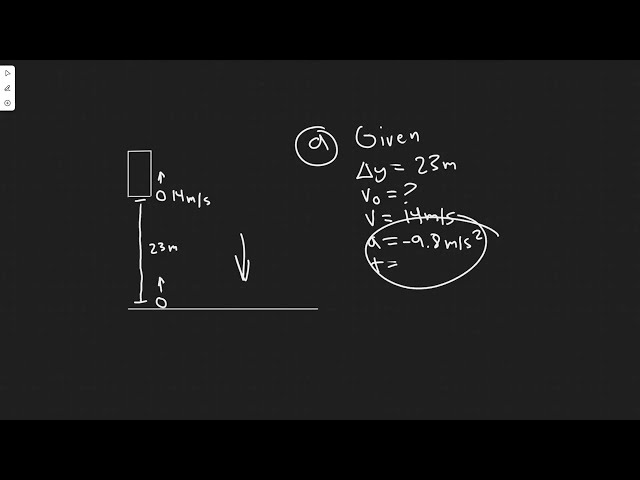A Baseball Is Thrown From Point S?

Have you ever wondered how a baseball is thrown from point S? Well, wonder no more! In this blog post, we’ll explore the science behind this phenomenon.

Introduction

In baseball, when a pitcher throws the ball to a catcher, the catcher tries to “frame” the ball in order to make the ball appear as close to the strike zone as possible. In other words, the catcher tries to trick the umpire into thinking that the ball is closer to the strike zone than it actually is. This can be done by holding the ball in a certain way or by using body language to create the illusion that the ball is closer than it really is.

The Physics of a Baseball Throw

A baseball throw is a parabola. You can determine the height, speed, and distance of the ball by the angle of release and the velocity of the throw. The ball will go the farthest when it is thrown at a 45 degree angle with a high velocity.

The Forces Acting on the Baseball

Anytime something is in motion, there are forces acting upon it. The same is true when a baseball is thrown. The faster the baseball is moving, the more force it has. When a pitcher throws a baseball, there are several forces acting upon the ball. The first is gravity. Gravity is the force that pulls objects towards the center of the Earth. It is constantly pulling on the baseball, trying to make it fall to the ground.

The second force acting on the baseball is air resistance. Air resistance is a type of friction that works against an object that is moving through the air. The faster an object moves through the air, the more air resistance it will have. Air resistance will slow down a baseball as it travels through the air.

The third force acting on the baseball is friction between the ball and the pitcher’s hand. This friction gives the pitcher more control over where he throws the ball and how fast it goes when it leaves his hand. Without this friction, pitchers would have a harder time throwing strikes!

The Equations of Motion

When a baseball is thrown, the pitcher exerts a force on it in the direction of the target. The ball then accelerates in that direction. After it is released, the only force acting on the ball is gravity, which causes it to fall straight down toward the ground.

The motion of a projectile can be described by the equations of motion:

x = x0 + v0t + 1/2 at^2

y = y0 + v0t – 1/2 gt^2

where x and y are the horizontal and vertical coordinates of the projectile, x0 and y0 are the coordinates of its point of release, v0 is its initial velocity, a is its acceleration, and g is the acceleration due to gravity (9.8 m/s2).

The Mathematics of a Baseball Throw

A baseball is thrown from point 𝑆 on a level field with an initial velocity of 𝑣 feet per second. The point 𝑆 is 𝑥 feet from home plate, and the point where the ball is caught is 𝑦 feet from home plate. Use the equation below to find how many feet the ball was thrown.

The Trajectory of the Baseball

As the baseball is thrown, it will follow a curve that is determined by its initial velocity and the force of gravity. The faster the ball is thrown, the more it will curve. If the ball is thrown horizontally, it will travel in a straight line. However, if the ball is thrown at an angle, it will follow a curved path.

The trajectory of the baseball can be described by a parabolic equation. This equation takes into account the initial velocity of the ball, as well as the force of gravity. The parabolic equation can be used to determine where the ball will land when it is thrown from point S.

The parabolic equation can be solved for any given point on the baseball’s trajectory. For example, if we want to know where the baseball will be five seconds after it is thrown, we can plug in t = 5 into the equation. This will give us the x and y coordinates of the baseball at that time.

The Flight Time of the Baseball

Assuming the baseball is thrown in a perfectly horizontal fashion, the flight time can be determined by calculating the time it takes for the ball to reach its maximum height. This can be done by using the equation:

t = (2 * v) / g

Where:
t = time (in seconds)
v = velocity (in meters per second)
g = acceleration due to gravity (9.81 m/s^2)

For a baseball thrown with a velocity of 40 m/s, the flight time would be:

t = (2 * 40) / 9.81
t = 8.16 seconds

Conclusion

The answer to this question is yes, a baseball can be thrown from point S. There are a few things to keep in mind when doing so, however. The first is that the person throwing the ball will need to have a good arm length; otherwise, the ball will not travel very far. Second, the person throwing the ball will need to put some spin on it; otherwise, it may not travel in a straight line. Finally, the person throwing the ball will need to aim for a specific point; otherwise, the ball may not go where they want it to.