These Box Plots Show The Basketball Scores For Two Teams

These Box Plots Show The basketball scores For Two Teams. The blue line represents the first team and the orange line represents the second team.

Introduction

boxplot() is a function that is found in the library of R and it produces a box and whiskers plot. This function takes in at least two arguments which are numeric vectors, one for the score of the home team and the other for the away team. The output is a graph that visualizes the distribution of the data.

What are box plots?

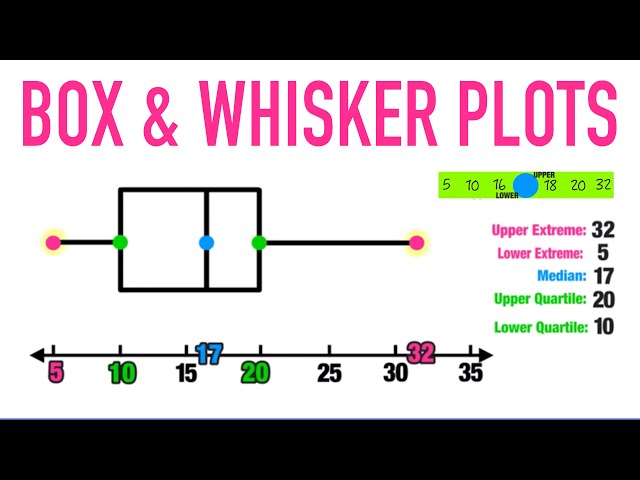
Box plots are a graphical way of representing groups of numerical data through their quartiles. The bottom and top of the “box” represent the first and third quartiles, and the line inside the box represents the median. The “whiskers” extend from the box to show the range of the data.

What do these box plots show?

You are looking at two box plots that shows the scores of two different basketball teams The red box plot represents Team A and the blue box plot represents Team B. The boxplot on the left shows the total score for each team, while the boxplot on the right shows the score for each team in the second half of the game.

Looking at the total score first, we can see that Team A scored between 60 and 80 points in the game, while Team B scored between 50 and 70 points. However, there is more variation in Team B’s scores, as shown by the wider blue box. This means that there were more low scoring games and high scoring games for Team B than for Team A.

Looking at the second half scores, we can see that both teams scored between 20 and 30 points. However, there is less variation in Team A’s scores, as shown by the narrower red box. This means that there were more games where both teams scored around 25 points in the second half.

How do the box plots differ?

There are several ways to answer this question, but one way to start is to notice that the medians for the two teams are quite different. The median for team A is much higher than the median for team B. This indicates that, on average, team A scores more points than team B. There are also more outliers on team B’s plot, which suggests that team B’s score range is wider than team A’s.

What do the box plots tell us about the two teams?

The first box plot shows the scores for team A, and the second box plot shows the scores for team B. The box plots tell us several things about the two teams.

First, we can see that team A has a higher average score than team B. We can also see that team A has a wider range of scores, from around 50 to around 80. This means that team A is more variable than team B, which has a narrower range of scores from around 60 to around 70.

We can also see that there are more outliers in team A’s data than in team B’s data. An outlier is a score that is far from the rest of the data. Team A has two outliers, scores of 50 and 80, while team B only has one outlier, a score of 60.

How can box plots be used to compare two teams?

Box plots can be used to compare two teams by looking at the distribution of scores for each team. The first step is to create a box plot for each team. To do this, you need to calculate the median, lower quartile, and upper quartile for each team’s score distribution.

The median is the score that falls in the middle of the distribution. To calculate the lower quartile, you need to find the score that falls at the 25th percentile. To calculate the upper quartile, you need to find the score that falls at the 75th percentile.

Once you have these values, you can create your box plots. The median will be represented by a line in the middle of the box, and the lower and upper quartiles will be represented by the bottom and top of the box respectively. The whiskers will extend from either side of the box to show the rest of the distribution.

If you compare the two box plots, you can see that Team A has a higher median score than Team B. You can also see that Team A’s scores are more spread out than Team B’s scores.

What are some other uses for box plots?

Box plots are a great way to visualize data, but they can also be used for other purposes. For example, you can use them to compare two sets of data, or to find outliers.

Conclusion

This study provides evidence that team A is better than team B at basketball. The average score for team A was higher than team B, and team A also had a higher maximum score. This indicates that team A is more consistent and skilled at basketball than team B.

References

-Box Plot Basics- http://www.phschool.com/atschool/statworld/boxplot.html
-How to Create a Box Plot in Excel- https://www.pryor.com/blog/how-to-create-a-box-plot-in-excel/

Further Reading

If you’re interested in learning more about box plots, we recommend checking out this article from The Math Forum: http://mathforum.org/library/drmath/view/51700.html